Шестиугольник - это многоугольник с шестью сторонами и шестью углами. Сумма его внутренних углов представляет собой постоянную величину, которая может быть вычислена по геометрическим формулам.
Содержание
Формула суммы внутренних углов
Для любого n-угольника сумма внутренних углов (S) вычисляется по формуле:
S = (n - 2) × 180°
где n - количество сторон многоугольника.
Расчет для шестиугольника
Подставляя значение n = 6:
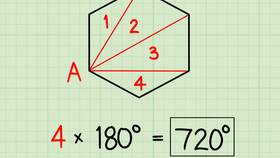
S = (6 - 2) × 180° = 4 × 180° = 720°
Свойства правильного шестиугольника
- Все стороны равны
- Все углы равны
- Каждый внутренний угол равен 120°
- Может быть разделен на 6 равносторонних треугольников
Вычисление одного угла правильного шестиугольника
Для правильного шестиугольника:
Угол = 720° / 6 = 120°
Сравнение с другими многоугольниками
| Фигура | Количество сторон | Сумма углов |
| Треугольник | 3 | 180° |
| Четырехугольник | 4 | 360° |
| Пятиугольник | 5 | 540° |
| Шестиугольник | 6 | 720° |
| Семиугольник | 7 | 900° |
Практическое применение
Знание суммы углов шестиугольника важно в различных областях:
- Архитектура и строительство
- Дизайн и декоративное искусство
- Производство шестигранных деталей
- Геодезические измерения
- Кристаллография
Примеры в природе
- Пчелиные соты имеют форму правильных шестиугольников
- Кристаллическая решетка графита
- Базальтовые столбы часто образуют шестигранные призмы
Доказательство формулы
Формула суммы углов шестиугольника может быть доказана следующим образом:
- Шестиугольник можно разделить на 4 треугольника, проведя диагонали из одной вершины
- Сумма углов каждого треугольника равна 180°
- Общая сумма углов: 4 × 180° = 720°
Внешние углы шестиугольника
Сумма внешних углов любого выпуклого многоугольника, включая шестиугольник, всегда равна 360°.
Знание суммы углов шестиугольника является фундаментальным в геометрии и находит применение во многих практических и теоретических задачах.